December 1999
MA214 : DISCRETE MATHEMATICS

QUESTION 3

Total Marks: 15 Marks

• Question 1
• Question 2
• Question 4
• Question 5
• Cover Page

SUGGESTED SOLUTIONS
Solutions and allocated marks are indicated in green.
Return to Question 3

(i)Suppose n =1 (mod 3 ). By writing n =3 k +1,where k is an integer,show that =1 (mod 3 ).[2 marks ]

One mark .
It follows that =1 (mod 3 )One mark .

(ii)Suppose n =2 (mod 3 ).Calculate (mod 3 ).[2 marks ]

We may write n =3 k +2 One mark .
Then , and so it follows that =1 (mod 3 )One mark .

(iii)Use (i)and (ii) to prove the implication “if n is an integer not divisible by 3,then =1 (mod 3 )”.[3 marks ]

If n is not divisible by 3 then either n =3 k +1or n =3 k +2 One mark. In each case, =1 (mod 3 ) One mark. Hence,“if n is an integer not divisible by 3, then =1 (mod 3 )One mark.

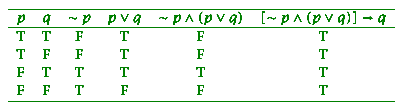
Show that [~p(p V q )] -> q is a tautology by constructing a truth table.

Award two marks for a completely correct truth table, subtract one mark for each mistake up to a maximum of two. Award one mark for noting all entries in last column are T and so it is a tautology.

Using algebraic laws show that ~((~pq ) V (~p~q )) V (pq )= p