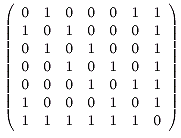| (a) |
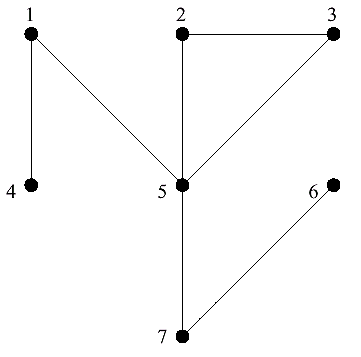
Show that every tree with at least two vertices has at least one vertex of odd degree. If every vertex were of even degree then since trees are connected (one mark )the tree would have an Euler cycle (one mark ). Since trees have no cycles at all,this cannot happen (one mark ).
|
[3] |
| (b) |
The following is an adjacency matrix of a graph. Draw the graph.
Three marks,subtract one for each mistake up to a maximum of three.
|
[3] |
| (c) |
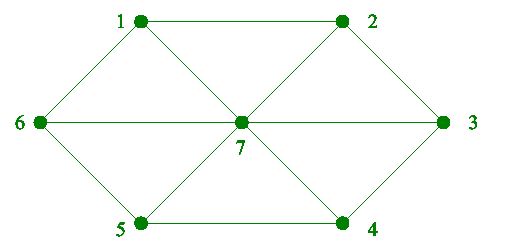
Consider the graph shown below.
(i)Write down the distance matrix.[2 marks ]
Two marks, Subtract one for each mistake up to a maximum of two. (ii)Define a walk, a trail and an Eulerian trail of a graph .Find an Eulerian trail in the given graph.[4 marks ] A walk is a sequence
of vertices
|
[6] |
| (d) |
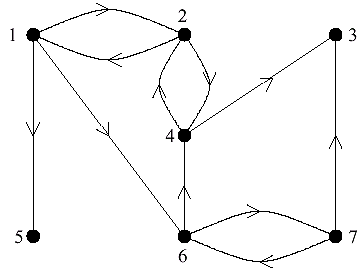
Consider the directed graph shown below.
Write down the adjacency matrix for this graph.
Three marks, subtract one for each mistake up to a maximum of three. |
[3] |
of
G where 
is
an edge of G. One mark .
