Dec1999 MA214 : Discrete Mathematics (Question 5)Suggested Solutions

(a)

How many bit strings of length eight either start with a 1 bit or end with the two bits 00?

Constructing a bit string of length eight beginning with a 1 bit can be done in =128 ways One mark .Constructing a bit string of length eight ending in 00 can be done in =64 ways One mark .Both tasks can be done in =32 ways One mark . Consequently,the number of bit strings of length eight that begin with a 1 and end with 00 is given by 128 +64 -32 =160 One mark .

[4]

(b)

Assume that in a group of six people, any pair of individuals consists of either two friends or two enemies. Show that there are either three mutual friends or three mutual enemies in the group.

Let A be one of the six people. Of the other five people in the group, there are either three or more friends of A, or three or more enemies of A (one mark )which follows from the generalised pigeonhole principle (one mark ). In the former case, suppose B, C and D are friends of A. If any two of these three individuals are friends then these two and A form a group of three mutual friends (one mark ). Otherwise B,C and D form a set of mutual enemies (one mark ). The proof for the later case follows similarly (one mark ).

[5]

(c)

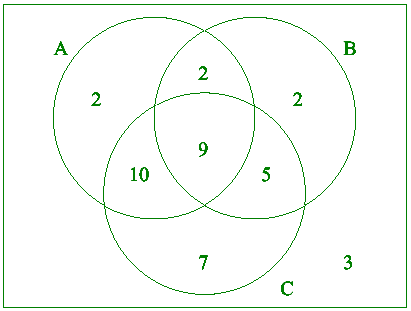
A study was carried out to determine the efficiency of three different drugs A,B and C in relieving headache pain.The following results were obtained:

40 subjects were given the chance to use all three drugs
23 reported relief from drug A
18 reported relief from drug B
31 reported relief from drug C
11 reported relief from both drugs A and B
19 reported relief from both drugs A and C
14 reported relief from both drugs B and C
37 reported relief from at least one of the drugs

Note that some of the 23 subjects who reported relief from drug A may have also reported relief from drugs B or C, with similar remarks applying to other data.

(i)How many people got relief from none of the drugs?[1 mark ]

The number of people that got no relief is equal to the number of people in the class minus the number of people that got some relief from at least one of the drugs,or 40 -37 =3(one mark ).[1 mark ]

(ii)How many people got relief from all three drugs?[2 marks ]

|A |+|B |+|C |-|A n B |-|A n C |-|B n C |+|A n B n C |=|A B C |(one mark)
so the number of people getting relief from all three drugs was 9 (one mark ).

(iii)Let A be the set of all subjects who got relief from drug A,B the set of all subjects who got relief from drug B,and C the set of all subjects who got relief from drug C.Make a copy of the diagram shown below and fill in the numbers for all eight regions.[2 marks ]

Two marks, subtract one for each mistake up to a maximum of two.

(iv)How many subjects got relief from A only?[1 mark ]

[6]